1. Linear Equations in Linear Algebra - 2

1.3 Vector Equations

 

이 장에서는 벡터를 포함하는 방정식을 일반 연립 방정식에 연결한다.

e 6. vectors with two entries

위 수식과 같이 entry가 두개인 벡터들을 vectors in $ {\mathbb{R}}^{2}$라고 하며, 여기서 $\mathbb{R}$은 실수 체계 real space, 2는 차원 공간을 나타낸다. 각각의 벡터들은 대응하는 원소들끼리 일치할 때 같은 벡터이며 순서가 있기 때문에 순서가 바뀌면 동일한 벡터가 아니다.

주어진 $\mathbb{R}$의 두 벡터 u와 v의 합(vector summation)은 각각의 대응하는 값들을 더해서 얻어진 벡터 u+v이다. 벡터 u의 c 스칼라 곱(scalar multiplication)은 각각의 원소들에 c를 곱해서 얻어지는 벡터 cu이다.

f 1. The parallelogram rule

Parallelogram Rule for Addition
If u and v in $ {\mathbb{R}}^{2}$ are represented as points in the plane, the u+v corresponds to the fourth vertex of the parallelogram whose other verices are u, 0, and v.

$ {\mathbb{R}}^{2}$의 u와 v가 평면의 점으로 표시되는 경우, u+v는 다른 꼭짓점이 u, 0, v인 평행사변형의 네번째 꼭짓점에 해당된다.

f 2. typical multiples of u, the set of all multiples of u

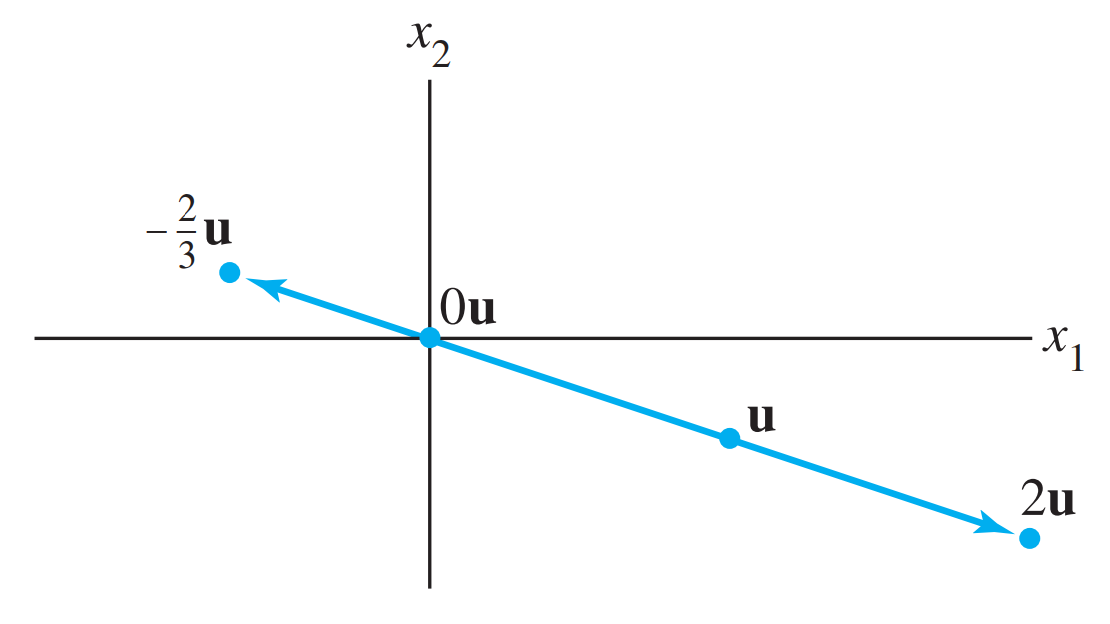
벡터 u의 특정 스칼라 곱은 좌측 그래프의 점처럼 표현될 수 있으며 벡터 u의 모든 스칼라곱 집합은 직선으로 표현된다.

f 3. vector scalar multiples in $\mathbb{R}^{3}$

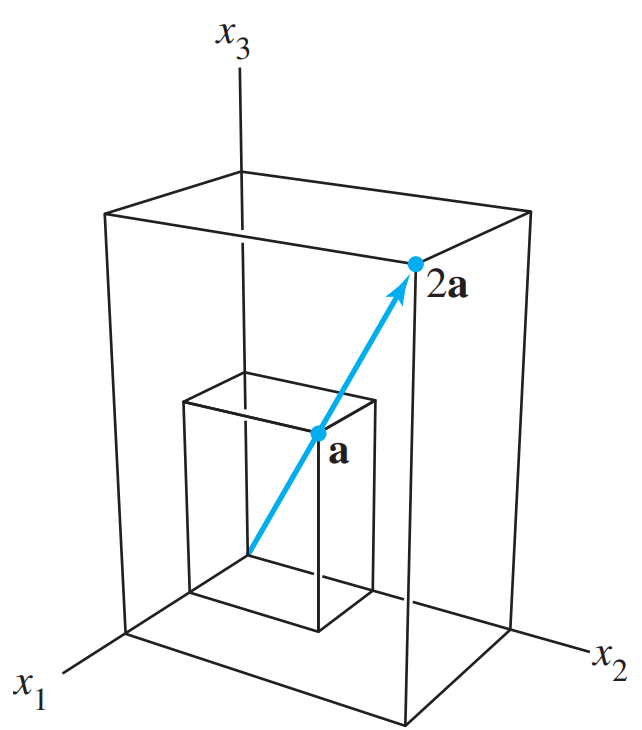
$ {\mathbb{R}}^{3}$의 벡터는 3개의 원소가 있는 3 x 1 열 행렬이다. 3차원 그래프에서 표현할 수 있으며 위 그래프에서 $a = \begin{bmatrix}2\\3\\4\end{bmatrix}$와 2a의 시각화를 확인할 수 있다.

n이 양의 정수이면 ${\mathbb{R}}^{n}$은 일반적으로 다음과 같이 n x 1 열 행렬로 작성되는 n개의 실수 리스트의 모든 집합을 나타낸다.

$$\mathrm{u} =\begin{bmatrix}u_{1}\\u_{2}\\\vdots\\u_{n}\end{bmatrix}$$

원소가 모두 0인 벡터는 zero vector라고 불리며 0으로 나타낸다.

Algebraic properties
For all $\mathrm{u}$ , $\mathrm{v}$ , $\mathrm{w}$  in $ {\mathbb{R}}^{n}$ and all scalars $\mathit{c}$ and $\mathit{d}$ :
  (i) $\mathrm{u}$ + $\mathrm{v}$ = $\mathrm{v}$ + $\mathrm{u}$                                               (v) $\mathit{c}$ ( $\mathrm{u}$ + $\mathrm{v}$ ) = $\mathit{c}$ $\mathrm{u}$+ $\mathit{c}$ $\mathrm{v}$
 (ii) ( $\mathrm{u}$ + $\mathrm{v}$ ) + $\mathrm{w}$  = $\mathrm{u}$  + ( $\mathrm{v}$  + $\mathrm{w}$ )                (vi) ( $\mathit{c}$ + $\mathit{d}$ ) $\mathrm{u}$ = $\mathit{c}$ $\mathrm{u}$  + $\mathit{d}$ $\mathrm{u}$
(iii) $\mathrm{u}$ + $\mathrm{0}$ = $\mathrm{0}$ + $\mathrm{u}$ = $\mathrm{u}$                                      (vii) $\mathit{c}$ ( $\mathit{d}$ $\mathrm{u}$ ) = ( $\mathit{c}$ $\mathit{d}$ ) $\mathrm{u}$
(iv) $\mathrm{u}$ + (- $\mathrm{u}$ ) = - $\mathrm{u}$ + $\mathrm{u}$ = $\mathrm{0}$                         (viii) $\mathit{1}$ $\mathrm{u}$ = $\mathrm{u}$
      where - $\mathrm{u}$ denotes (- $\mathit{1}$ ) $\mathrm{u}$

$ {\mathbb{R}}^{n}$의 대수학적 성질은 위와 같다.

이 중에서 (i)을 증명하는 과정은 다음과 같다.

$\mathrm{u}$ + $\mathrm{v}$ = ( $u_{1}$+$v_{1}$ , $\cdots$ , $u_{n}$+$v_{n}$ ) = ( $v_{1}$+$u_{1}$ , $\cdots$ , $v_{n}$+$u_{n}$ ) = $\mathrm{v}$ + $\mathrm{u}$

 

Linear Combination

$\mathrm{y} = \mathit{c_{1}}\mathrm{v_{1}} + \cdots + \mathit{c_{p}}\mathrm{v_{p}}$는 각각의 vector에 weight가 곱해져있는 선형결합으로 표현이 된다.

 

따라서

Is a vector b in Span {$v_{1}$, $\cdots$, $v_{p}$}?

와

Does the following vector equation have a solution?

$x_{1}v_{1} + x_{2}v_{2} + \cdots x_{n}v_{n}$

그리고

Does the following augmented matrix have a solution?

[$v_{1}$ $\cdots$ $v_{n}$ $\mathrm{b}$]

은 동일한 것을 물어보는 질문이다.

 

f4. Span {v}, Span {u,v} each as a line and plane through the origin

$ {\mathbb{R}}^{3}$에서 Span {$\mathrm{v}$}와 Span {$\mathrm{u}$, $\mathrm{v}$}를 기하학적으로 나타내면 위와 같이 각각 직선과 평면으로 표현된다.