선형대수학 공부 교재로는 Linear Algebra and its Applications 5th edition을 활용했다.
코세라 강의도 많이 추천 받았고 유튜브 강의도 들어봤는데
그냥 책 한 권 보고 싶기도 하고 강의도 있어서 골랐다.
첫번째 장은 Linear Equations in Linear Algebra, 즉 선형대수의 선형방정식에 대해 다룬다.
하버드의 Leontief 교수가 미국 경제를 표현하는 250,000개의 정보를 포함하는 데이터를 500 분야(ex. 산업별)로 나누고, 각 분야가 다른 분야에 기여하는 방식을 설명하는선형 방정식을 작성한다. 당시의 Mark 2 컴퓨터는 500개의 미지수로 이루어진 500개의 연립방정식을 연산할 수 없었기 때문에 Leontief 교수는 이 문제를 42개의 미지수로 이루어진 42개의 연립방정식으로 정리한다.
이 연산에 꼬박 56시간이 소요되었으며 1973년에 노벨 경제학상을 수상한 Leontief 교수가 경제학에서 수학적 모델링의 새로운 지평을 열었다고 평가된다. 굉장히 큰 정보가 포함되므로 모델은 주로 선형이며, 다른 말로 모델이 선형 연립 방정식으로 설명된다고 할 수 있다.
선형 연립 방정식은 선형대수학의 핵심이며 1 장에서는 선형대수학의 핵심 개념을 간단하고 구체적인 환경에서 공부한다.
1.1 Systems of Linear Equations

선형방정식은 b와 coefficient(계수)가 실수 혹은 허수 값을 가지는 위와 같은 식이다.


위와 같은 식은 선형방정식이 아니며 e1과 같은 형태로 표현될 수 없다.
선형 연립방정식은 같은 variable(변수)를 공유하는 선형 방정식들의 모음이다.
두 선형 연립방정식이 동일한 해를 가지면 equivalent(동치)하다고 한다.
연립방정식의 해는 방정식들의 replacement, scaling, interchange를 통해 구할 수 있다.



선형 연립방정식의 해는 여러개가 될 수도, 단 하나만 존재할 수도 있으며 이를 consistent하다고 하며, 해를 가지지 않을 때 inconsistent하다고 한다.
1.2 Row Reduction and Echelon Forms
이 장에서는 1.1 장에서 배운 것을 row reduction algorithm으로 발전시켜 어떤 선형연립방정식이라도 풀 수 있도록 한다.
알고리즘의 앞부분을 활용하여 fundamental existence와 uniqueness(존재와 고유성)에 대한 답을 구할 수 있을 것이다.
행렬이 augmented matrix의 형태이든 아니든 어떤 행렬에나 적용이 가능하다.
rectangular matrix는 다음 세 조건을 만족할 때 echelon form(사다리꼴 행렬)이다.
1. 모든 nonzero row들이 모든 값이 0인 행 보다 위에 위치한다.
2. 각 행의 leading entry가 윗 행의 leading entry보다 오른쪽에 위치한다.
3. leading entry 아래의 모든 요소는 0 값을 가진다.
echelon form이 다음 조건을 만족하면 reduced echelon form(행간소사다리꼴)이다.
1. 각각의 nonzero 행의 leading entry 값이 1이다.
2. 각각의 leading entry가 각 행의 유일한 nonzero 값이다.


Theorem 1. Uniqueness of the Reduced Echelon Form
Each matrix is row equivalent to one and only one reduced echelon matrix.
모든 reduced echelon form은 유일하며 이에 대한 증명은 4장에서 가능하다.
example 1

위 행렬을 elementary row operation을 통해 echelon form과 reduced echelon form으로 변환시켜라.
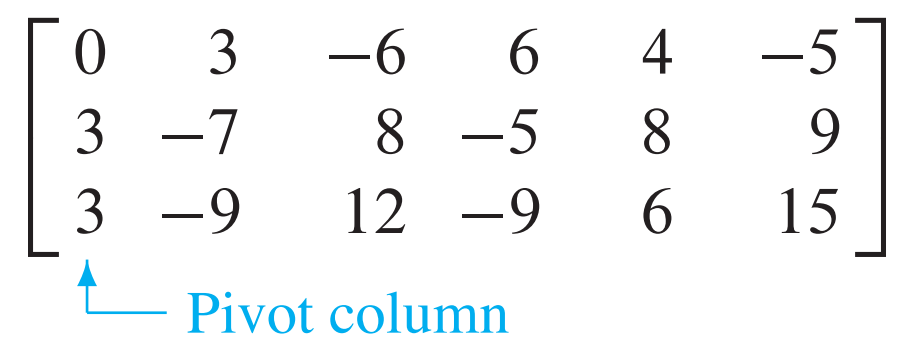

우선 가장 왼쪽의 nonzero column을 pivot column으로 두고 pivot position을 해당 칼럼의 최상단으로 둔다.
pivot column에서 nonzero entry를 pibot column에 두기 위해 필요하다면 interchange를 해준다.


pivot position 아래 값들이 모두 0이 되도록 처리해준다. 예시에서는 row 1을 row 2에서 빼준다.
새로운 pivot column을 정하고 pivot position도 정한다.


pivot postion 아래 값들이 모두 0이 되도록 row 2의 3/2 값을 row 3에서 빼주고
pivot 값을 옮겨준다.
이상의 과정이 row reduction algorithm의 forward phase라고 불리며 이후는 reduced echelon form을 만들어내는 backward phase라고 불린다.
pivot 값이 1이 아닌 경우 scaling 과정을 통해 1로 맞춰주고 예시에서는 이미 값이 1이기 때문에 생략한다.
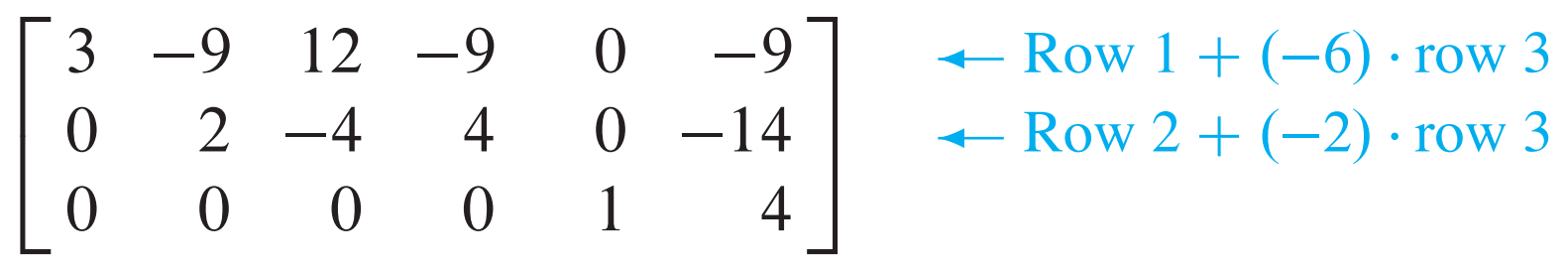
pivot 위의 값들을 0으로 만들어 주기 위해 row 1에는 row 3의 6배를 빼주고 row 2에는 row 3의 2배를 빼준다.

다음 pivot 값을 1로 맞춰주기 위해 scaling을 진행한다.

pivot 위의 값을 0으로 만들어주기 위해 row 1에서 row 2의 9배를 더해준다.

다음 pivot 값을 1로 맞춰주기 위해 scaling을 진행해서 최종적으로 reduced echelon form을 얻어낸다.
row reduction algorithm을 augmented matrix에 적용시켰을 땐 연립선형방정식의 해를 바로 구할 수 있다.

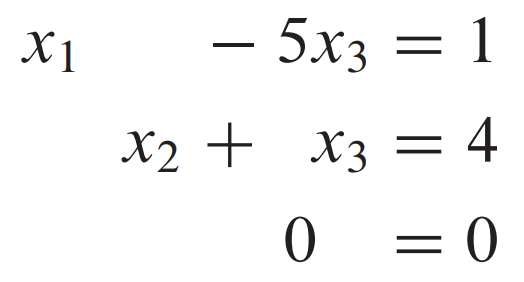

leading position에 해당되는 $x_{1}, x_{2}$는 basic variable(leading variable), $x_{3}$는 free variable이라고 불리며 나머지 변수는 free variable에 의해 표현된다.
Theorem 2. Existence and Uniqueness Theorem
A linear system is consistent if and only if the rightmost column of the augmented matrix is not a pivot column - that is, if and only if an echelon form of the augmented matrix has no row of the form
[ 0 ... 0 b] with b nonzero
If a linear system is consistent, then the solution set contains either (i) a unique solution, when there are no free variable, or (ii) infinitely many solutions, when there is at least one free variable.
augmented matrix의 가장 오른쪽 column이 피벗 칼럼이 아닐 때 선형 연립 방정식은 consistent 하다.
free variable이 하나도 존재하지 않는다면 연립 선형 방정식의 해가 단 하나 존재하고,
free variable이 하나 이상 존재면 무수히 많은 해가 존재한다.
'ML·DL > Linear Algebra' 카테고리의 다른 글
| 1 (0) | 2024.11.11 |
|---|---|
| 1. Linear Algebra - 4 (0) | 2024.11.10 |
| 1. Linear Algebea (0) | 2024.11.09 |
| 1. Linear Equations in Linear Algebra - 2 (0) | 2024.11.07 |
| 1. Linear Equations in Linear Algebra - 1 (5) | 2024.11.07 |
